





ա)
x^(12) – 1 = (x^(4) – 1) ⋅ A
Քանի որ x^(4) – 1 = (x^(2) – 1) ⋅ (x^(2) + 1), ապա
A = x^(2) – 1
բ)
x^(12) – 1 = (x^(2) + 1) ⋅ A
A = (x^(12) – 1) / (x^(2) + 1)
գ)
x^(12) – 1 = (x – 1) ⋅ A
A = (x^(12) – 1) / (x – 1)
դ)
x^(6) – 64 = (x – 2) ⋅ A
A = (x^(6) – 64) / (x – 2)
ե)
x^(5) – 32 = (x – 2) ⋅ A
A = (x^(5) – 32) / (x – 2)
զ)
x^(7) – 128 = (x – 2) ⋅ A
A = (x^(7) – 128) / (x – 2)
ա) (5n + 7) / n = 5 + 7 / n
Ուստի ցուցիչի աստիճանը՝ 1։
բ) (5n + 7) / (n + 1)
Քանի որ n-ի բարձրագույն աստիճանը 1 է,
ցուցիչի աստիճանը 1 է։
գ) (3n^(2) – 6n + 1) / n
Բաժանելով՝ 3n – 6 + 1 / n
Ուստի ցուցիչի աստիճանը 1 է։
դ) (7n + 5) / (n + 1)
Քանի որ n-ի բարձրագույն աստիճանը 1 է,
ցուցիչի աստիճանը 1 է։
ե) (2n^(2) – 6n + 7) / (n – 3)
Բարձրագույն աստիճանը 1 է։
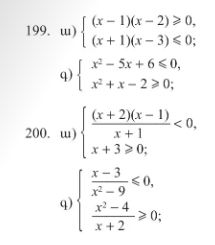
199) (ա)x∈[-1,1]U[2,3]
(գ)x∈[2,3]
200) (ա) x∈ [-3,-2> U <-1,1>

ա)x ∈(-4,-2)U(4,+∞)
գ)x∈<-∞,-3>u<3,4>U<4,+∞>

ա)x∈<-7,-3>
գ)x∈<-∞,-2>U<2,5>
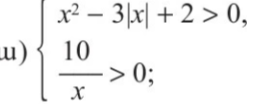
ա)x∈<0,1>U<2,+∞>
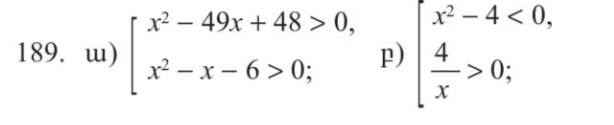
ա)x∈<-∞,-2>U<48,-∞>
բ)x∈<0,2>